Comprehensive List

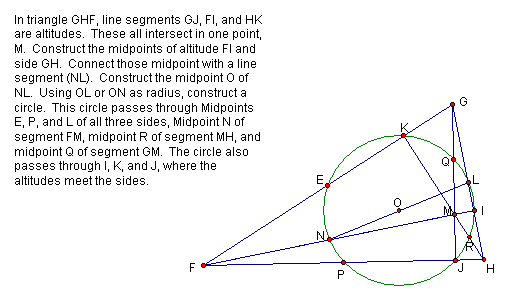
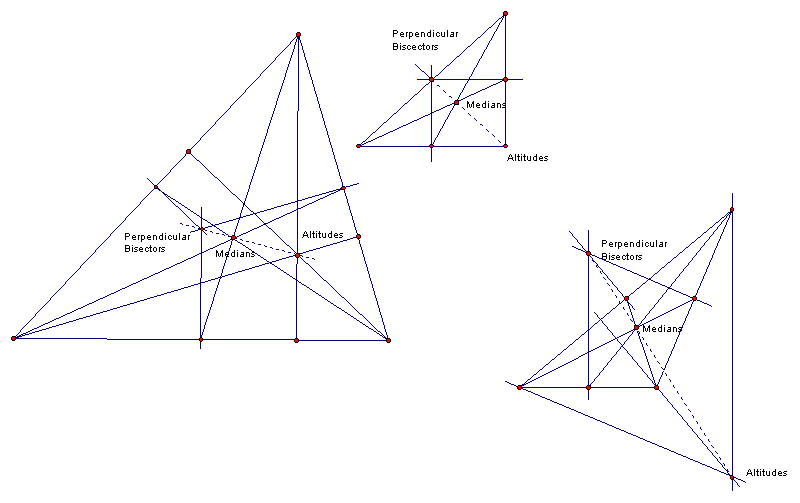
The altitudes (perpendiculars from a vertex to the opposite side) all meet at one point. (The dashed lines show an overlap of triangle sides and altitudes, or an extension of a triangle side. The triangles are the lines that directly connect the points.

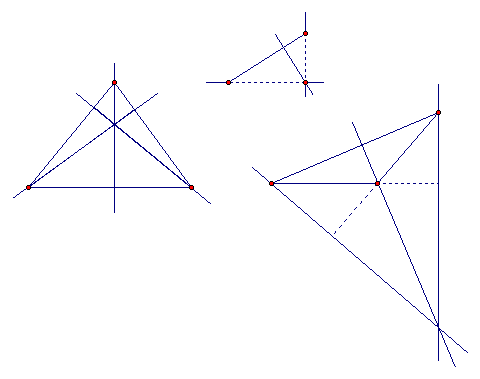
The medians of any triangle (a line segment from a vertex to the opposite side that divides the opposite side into two equal segments meet in a point that is two thirds the distance. Ex: if NF equals 1, then BN equals 2.

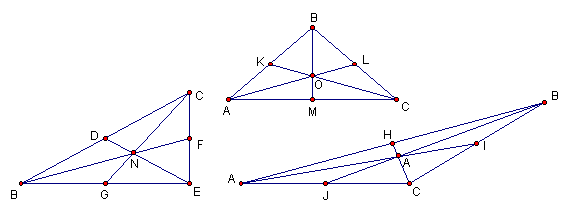
In any triangle ABC, the perpendicular bisectors of any two or three sides will meet in one point that is equidistant from all three points. Call this point D. You can draw a circle around center D with radius DB and it will intersect all of the points in the triangle. A figure is cyclic if there is a circle which can be drawn through all the points of the figure. Every triangle is cyclic, but every quadrilateral is not. The rule for polygons is that "if the perpendicular bisectors of all the sides meet at one point, then the polygon is cyclic.

In the third figure, triangle ABC is a right triangle. It is interesting to note that in a right triangle, the perpendicular bisectors meet on the midpoint of the hypotenuse (the longest side).

In any triangle ABC, the angle bisectors of any two or three angles will meet in a point (D) that is equidistant from all three sides of the triangle. If you draw a line segment DE perpendicular to line segment AC, and using D as center and DE as radius, a circle can be drawn which intersects all three sides of the triangle in exactly one point.

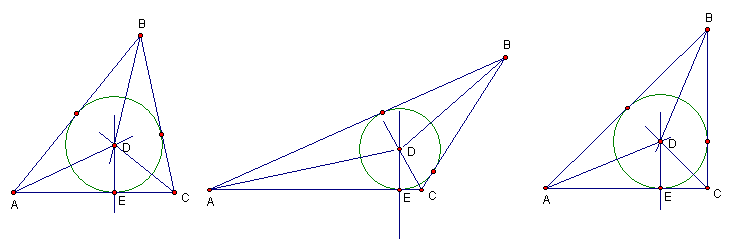
In circle A with diameter BC, any angle with any vertex (D, E, F, or G) and intersecting the circle at diameter BC is a right (90 degree) angle. It is also interesting to note that the angle bisector of any of these angles (one shown) intersects circle A at the same place that perpendicular bisector of BC intersects circle A.

 

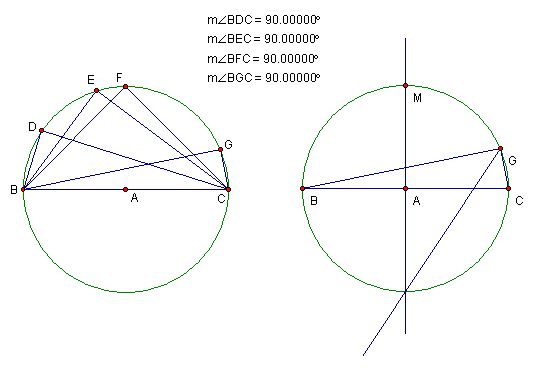
As the name suggests, I invented this theorem. My theorem is as follows:

1. When an angle is inscribed in a semicircle, it is a right angle.

2. AB is the diameter of circle C. Draw the perpendicular bisector of AB intersecting circle C at a point (not labelled).

3. Make the angle bisector of angle ADB. It intersects the circle at the same point as the angle bisector in "step 2"

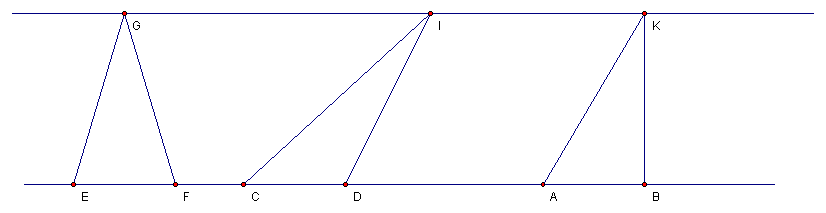
If lines GI and EB are parallel, and EF equals CD which equals AB, then the triangles have equal area.

 

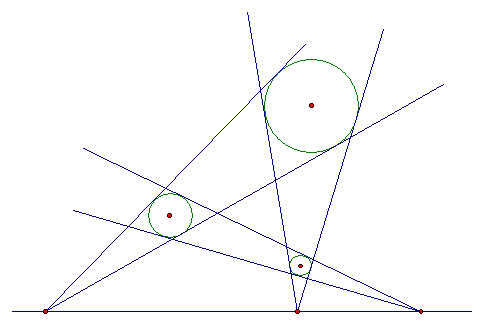
The common tangents to three circles meet on a straight line. This theorem was discovered by a mathematican by the last name of Monge.

 

If triangle ABC is a right triangle, then the measure of the two shorter sides (called legs) squared and added together equals the square of the measure of the hypotenuse. (a squared + b squared = c squared).

In this case, AB = 4, BC = 3, and AC = 5.

4 squared = 16,

3 squared = 9

5 squared = 25

16 + 9 = 25.

 

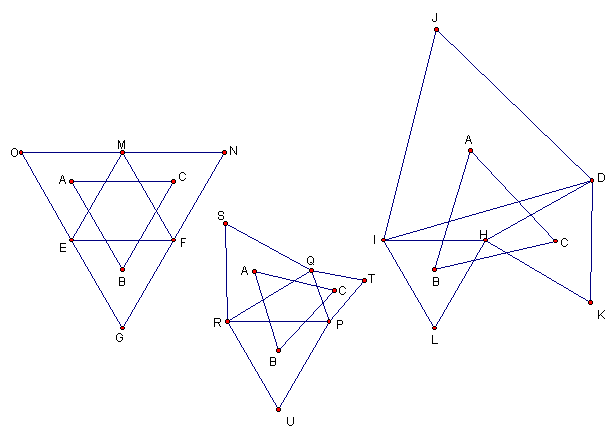
If on any triangle's (MEF, QRP, or DIH) sides equilateral triangles are constructed, ((OME, MNF, EFG), (SRQ, TQP, URP), or (JID, LIH, KHD), and the center of these triangles are found, (A, B, and C). Then triangles ABC are equilateral.

SAS stands for Side Angle Side. The "SAS Triangle Area Conjecture" as it is called by my source is

Area = 1/2 ab sin C

where "Area" equals the area of the triangle. "a" and "b" are any two sides of a triangle and C is the angle between them.

For more information see my Calculations page or my Geometrical Formula's page.

 

In any triangle, the perpendicular bisectors, the medians, and the altitudes meet at one point each. If you connect these points, you will get a straight line, represented here as a dashed line. This line was discovered by a mathematician by the name of Euler.

Click here to return to Ian's Geometry Forum.