The geometric mean is a suprisingly useful property of segments. Parts of right triangles, especially when an altitude to the hypotenuse is drawn are often in geometric mean proportion. The geometric mean is the form

a/x = x/b

where x is the geometric mean. Or

x = SquareRt(ab)

where x is the geometric mean.

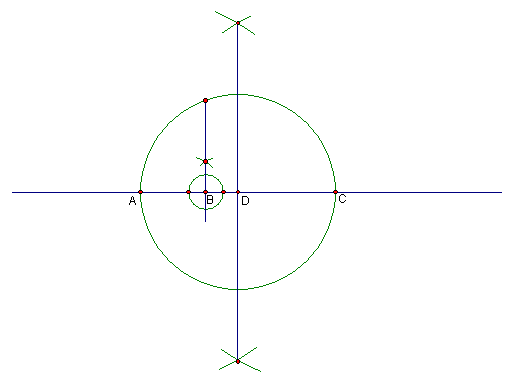
To construct the geometric mean of two segments AB and BC, draw them together on the same line as shown and find the bisector of AC. This can be done with a perpendicular bisector as shown, or with a compass. Call the bisector of AC "D". Draw a circle with radius DA or DC. Where segments AB and BC meet at B, draw a perpendicular through B perpenndicular to AC. Where it intersects the circle put a point. B to this point is the geometric mean between AB and BC.

Click here to return to Ian's Geometry Forum.