Approximate Construction of Regular Polygons
Ian Mallett, Brenda Mallett, Russell Mallett, May 22, 2006
Abstract:
Some regular polygons with n sides are classically "constructible" using only a compass and a straightedge, while others have been proven by Gauss to be "unconstructible" in the exact sense. We develop a practical general procedure for the approximate construction of regular polygons which works well for large n and which can be adapted for small n.
Introduction:
Ian, 14, an 8th grade geometry student taught at home, has been interested in finding approximate and practical ways to construct regular polygons that are impossible to construct exactly if using only a compass and straightedge.
Accordingly, he played around with the geometry computer program "Geometer’s Sketchpad" until he discovered a way to create an approximate regular heptagon (7-sided polygon.) For comparison, other procedures for doing this have been described by Dixon (Mathographics. New York: Dover, 1991, reprinted at http://mathworld.wolfram.com/Heptagon.html).
He then extended his method for nonagons, with results that also compare favorably with those shown by Dixon (http://mathworld.wolfram.com/Nonagon.html).
Ian then generalized the method for polygons of any n. Analysis by relatives with more math experience refined this result to a simple procedure with excellent accuracy.
Discussion:
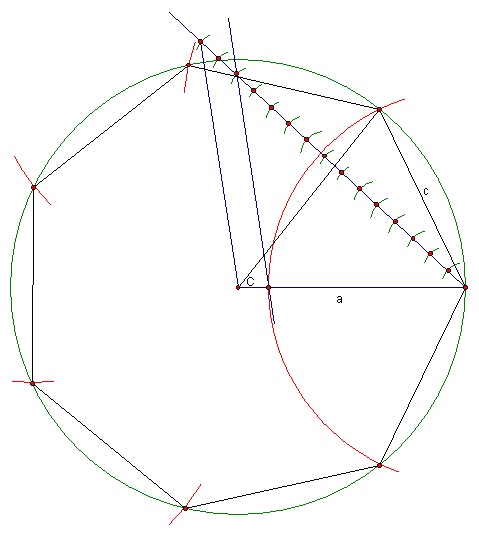
To replicate Ian's initial efforts, using standard geometric techniques, one may draw a circle of radius a, then divide the radius of the circle into 15 segments of equal length. Then, using a compass set to c=13/15 of the radius, one may mark off arcs around the circumference of the circle and connect the intersections to inscribe an almost-regular heptagon, with central angles only about 0.07 degrees too small.
At this point, Ian received kind encouragement from Harold Jacobs, author of his favorite textbook, Geometry: Seeing, Doing, Understanding (3rd edition). Jacobs suggested we evaluate the figure using the Law of Cosines. Ian then set out to come up with a method for nonagons (9-sided polygons). Working with his mom, Brenda, he found that a fraction of the radius which seemed to work well was 13/19, for central angles even more accurate than the approximate heptagon’s – a little over 0.01 degrees too large each.
Suspecting a pattern, Ian generalized the procedure to the following and confirmed its usefulness for polygons with n>5:
Formula 1: To approximately construct a regular polygon of n sides, mark off side lengths around a circle with a fraction of its radius equal to 13/(2n+1).
Following up on Jacobs' idea, Ian and Brenda worked with the Law of Cosines to evaluate this formula for various n.
The Law of Cosines states:
c2=a2 + b2 – 2abcosC,
Where a, b, and c are the sides of a general triangle and C is the angle opposite side c.
In the case of Ian’s “fraction of the radius” procedure, both a and b are the radius of the circle, and c represents the length of one side of the polygon. C is the central angle opposite c, and for a regular polygon of n sides is equal to 360/n, or in radians 2π/n.
Since the number of interest for construction is the polygon side length c divided by the radius of the circle a, one may solve the Law of Cosines for the fraction c/a:
c/a=√(2*(1-cosC))
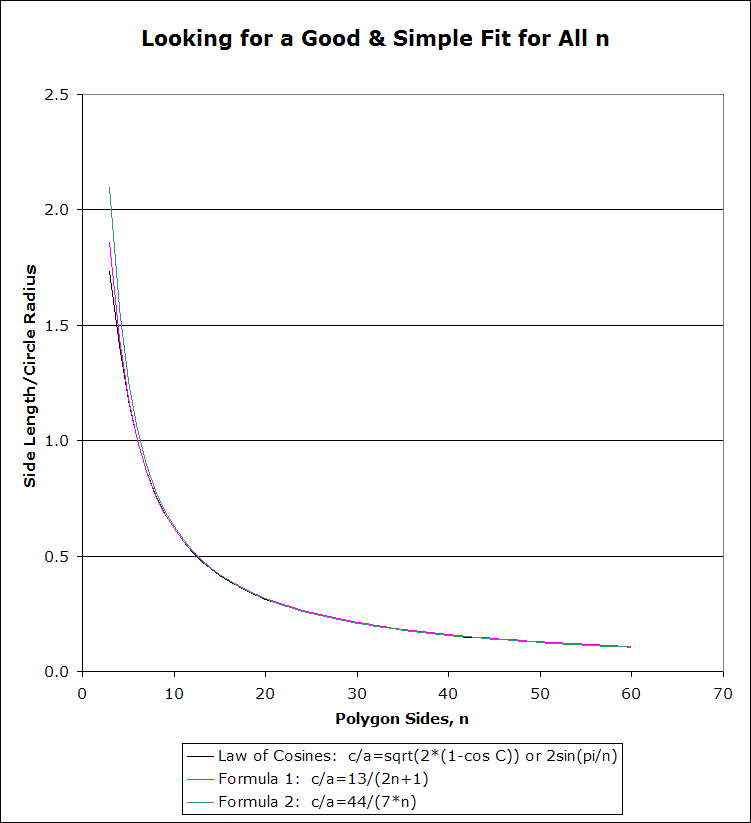
A quick comparison in Excel of this desired c/a with that given by 13/(2n+1) for increasing n shows that the approximation is a remarkably good fit for such a simple formula.
Note that Formula 1 works exactly for a hexagon and extremely well for nonagons. The individual central angles constructed become less accurate up to n=23, although they are still accurate to within a quarter of a degree, then very slowly improve for remaining n; however, the improvement is overcome by the multiplicative effect of increasing n, so that for the polygon as a whole the cumulative error slowly increases with n.
Brenda then consulted with Ian's grandfather, Russ Mallett, a retired mathematician, to review the 13/(2n+1) approximation and to comment on why it fit the desired c/a so well.
Russ pointed out that, using the trig identity (1-cosC)=(2sin2C), our rearranged Law of Cosines becomes (using C in radians):
c/a=2sin(π/n)
Further, for small central angle C (i.e., large n),
sin(π/n) = π/n (approximately), so
c/a=2(π/n) for large n
Equating 13/(2n+1) to this and solving for π, one finds that, for large n, we were essentially using the ratio 13/4 as an approximation of π (at large n one may ignore the contribution of the +1).
Using a common, better fractional approximation of π (22/7), and running it back through, one gets another “fraction of the radius” formula for practical regular polygon construction:
Formula 2: c/a=44/7n for large n
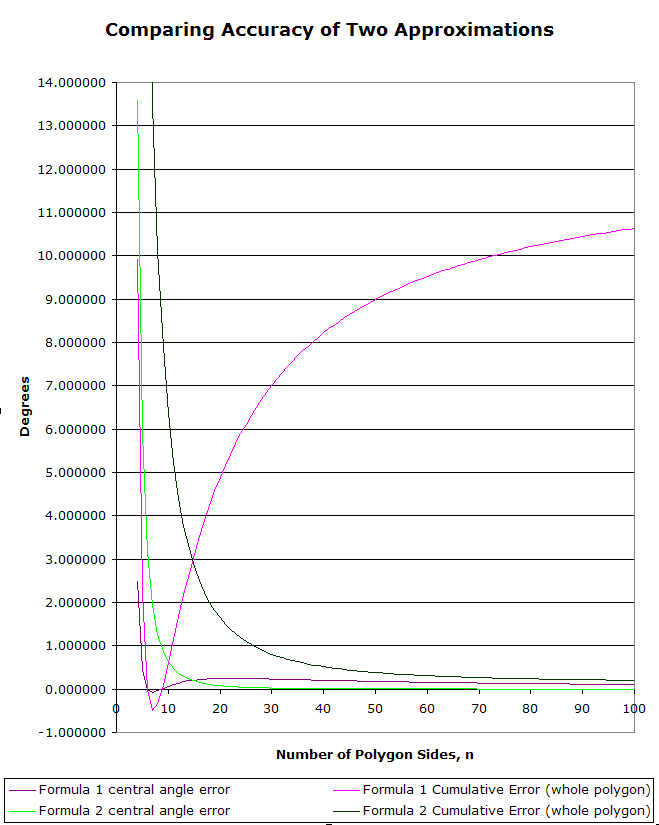
(One might use another approximation for π, such as 355/113, but the physical compass and straightedge procedure would quickly become unrealistic, with only a small gain in accuracy.) Although both are good, Formula 2 is much better than Formula 1 for n>14 (see graphs, below). For example, for n=25, Formula 1 results in central angles more than 0.24 degrees too large, for a cumulative error over the 25 angles of over 6 degrees, while Formula 2 results in central angles just over 0.04 degrees too large, for a cumulative error of only a litle over 1 degree.
In contrast to Formula 1, Formula 2 only improves with increasing n, for both individual central angles and for polygons as a whole.
Note: For the second graph comparing errors, I did not include n=3. Both formulas are terrible for n=3, with central angles given by Formula 1 being over 16 degrees too large and those given by Formula 2 being over 17 degrees too small. Instead, I restricted the scale of the graph to a narrower range and included only values for n>3. In a practical sense, this is fine since we already have an exact construction for regular triangles one would be more likely to use.
After using common exact constructions for n=3,4, and 5, one might reasonably continue with the Formula 1 approximation for n=6 through 14, and Formula 2 for higher n. However, Russ suggests that, for a highly accurate polygon of small n, one could merely construct a polygon with a convenient integer multiple of n sides, but only connect a corresponding fraction of the vertices. Thus we have a procedure that covers polygons of all n.
It may be straining the bounds of practicality to suppose that someone setting out to construct polygons of moderately large n would reasonably begin by dividing a circle's radius into hundreds of segments, taking 44 of them as their polygon's side length. However, even if it might be somewhat time-consuming, Ian's "fraction of the radius" principle is at least straightforward and the accurate results possible are satisfying.
Conclusion:
We are pleased to have been able to posit a successful general rule for the approximate construction of regular polygons from Ian’s discovery of two special cases, which, when analyzed, yielded a new and improved relationship. Two other general methods for the approximate construction of polygons are given by the Encyclopedia Brittanica 11th edition (reprinted at http://encyclopedia.jrank.org/PIG_POL/POLYGON_Gr_rroXus_many_and_ywvi.html); a comparison of the errors among the three methods could be the subject of future work.