It is impossible to trisect any given angle, but it is possible to trisect certain angles. For example: You can trisect a 90 degree angle, but not a 60 degree angle. For a list of angles that can be trisected in 5-degree increments, click here. List of Trisectable Angles. Of course, sometimes, you have to know beforehand what the measure of the angle is. Basically, you construct an angle with a given measure that happens to trisect a given angle. Here is a list of constructable angles. Constructable angles.
The topic of trisecting angles is immense. Many constructions have been published that are incorrect. It is possible to trisect any angle, but it would take an infinite number of steps. It is also possible to trisect angles by estimating and checking. or by "sliding" a straightedge. However, it is absolutely impossible to trisect most angles by construction.
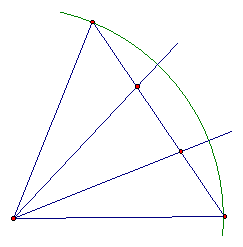
Here is one way to make an approximate construction for angle trisection.
Draw a line between the endpoints of the sides of the angle and trisect it. Draw rays between the angle's vertex and the points that trisect the line. Theoretically, these rays trisect the angle, but in reality THEY DO NOT.

There are many approximations of this, but all are inexact. Here are some more ways:
| Trisect 1 (Shown Above) | Trisect 4 | |
| Trisect 2 | ||
| Trisect 3 |
Click here to return to Ian's Geometry Forum.
Click here to return to Problems of Antiquity.